我的两分钱
2023-08-01
490
0
0
0
0
本文爲轉帖,原文鏈接如下,如有侵權,請聯繫我們,我們會及時刪除
原文鏈接:https://mp.weixin.qq.com/s/Xliq7LhcfQOFmSgDyfEDWA Tag: AI原理 神经网络
網站名稱:大白话说AI:没有数学推导,一图理解Weight Decay(权重衰减)如何解决过拟合
網站地址:https://mp.weixin.qq.com/s/Xliq7LhcfQOFmSgDyfEDWA
这是本系列的第11篇文章,在这个系列中,我将尝试尽量用大白话的方式,来解释一些AI领域的基本概念,我相信不论AI背后的数学有多复杂,其基本思路一定是清晰的,可以用数学无关的方式讲清楚的。在应用神经网络…
[SEO信息] [Alexa信息]
-->>直達網站
这是本系列的第11篇文章,在这个系列中,我将尝试尽量用大白话的方式,来解释一些AI领域的基本概念,我相信不论AI背后的数学有多复杂,其基本思路一定是清晰的,可以用数学无关的方式讲清楚的。
在应用神经网络时,我们常常碰到过拟合的问题,比如在下图中,我们想用一条线来拟合一些数据点的分布:
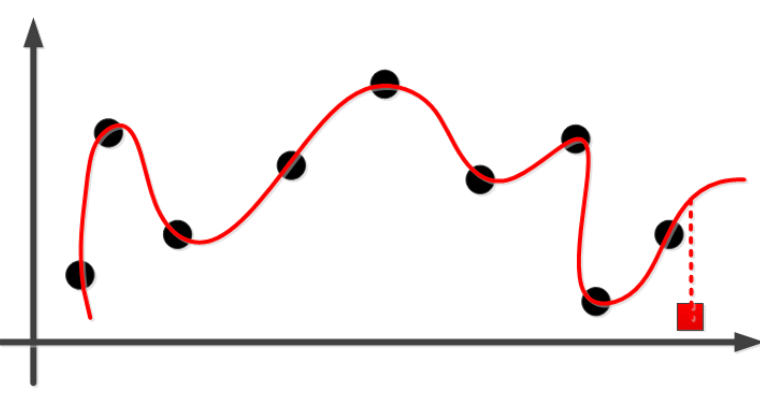
虽然对已知的数据点,这条线拟合的很完美,但对于未知的数据点(图中红色方块),则误差很大,这就是典型的过拟合,更好的拟合应该是类似下面这样:
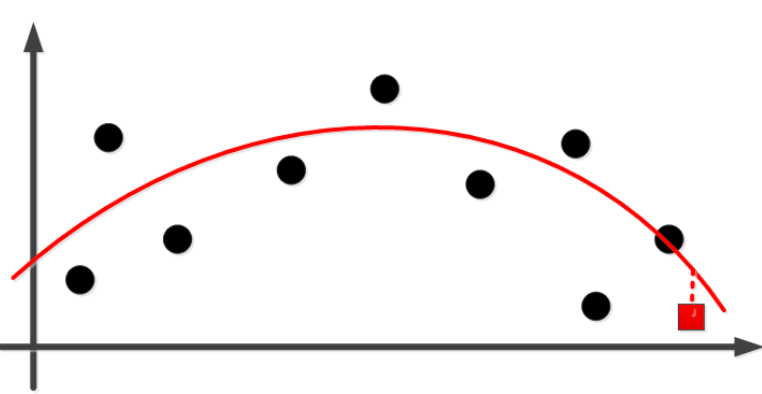
虽然对已知的数据点有一定的误差,但是对未知的数据点(图中红色方块)误差却较小。
那么我们如何来避免过拟合呢?一种思路是减小的模型复杂度,用更少的参数来训练模型,但参数过少往往导致模型无法捕捉数据中隐藏的复杂规律,出现欠拟合的情况:
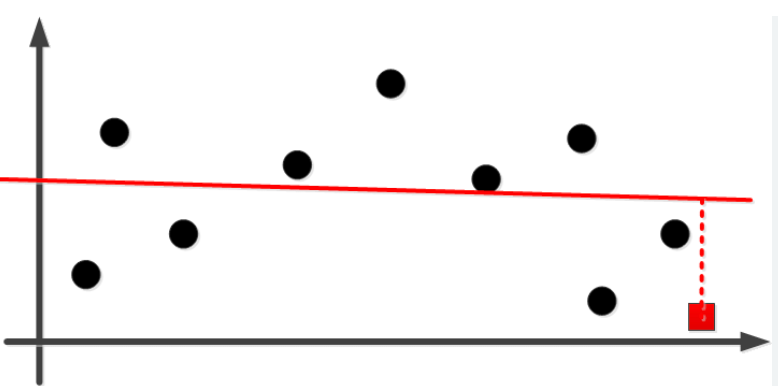
这种情况下模型对已知和未知的数据,误差都比较大。
那么有没有办法还是保持大量参数以捕获复杂的数据规律,同时还对能控制模型的复杂度呢?
解决办法就在细节中,下图是一个典型的神经网络示意图:
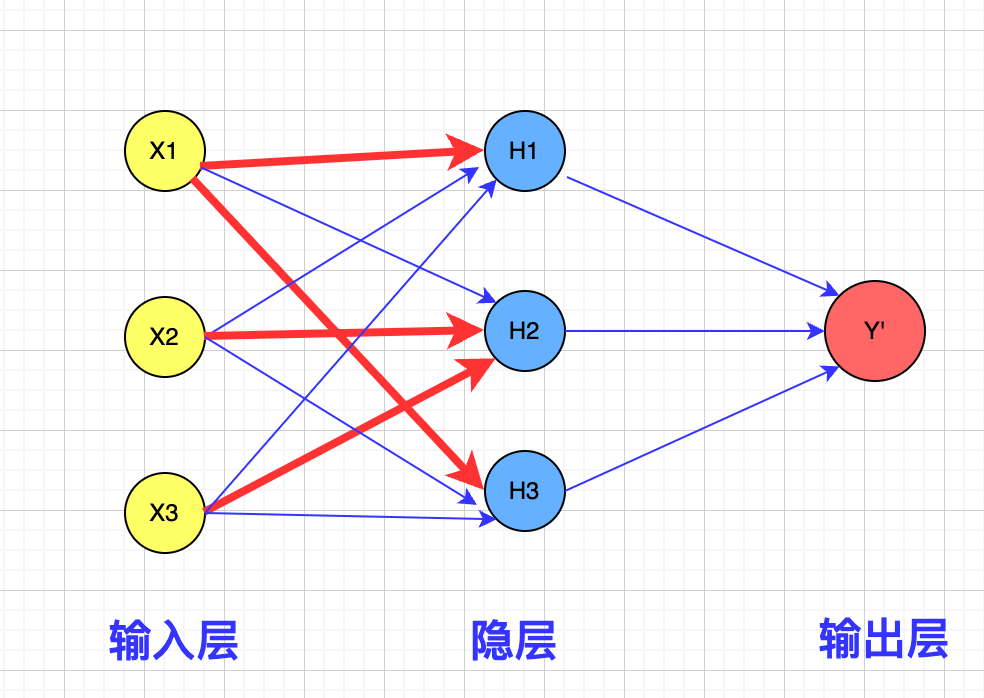
图中的箭头越粗,表示权重值越大,而权重值越大,则连接的神经元越容易被激活,神经元如果过于敏感,则很容易被数据噪声影响,通过降低神经元的敏感度,我们就可以屏蔽干扰信息,只捕获在数据中反复出现的模式,这样就可以有效避免过拟合了。
那么应该如何调节权重以降低神经元的敏感度呢?神经网络是通过反向传播误差来调节权重的:
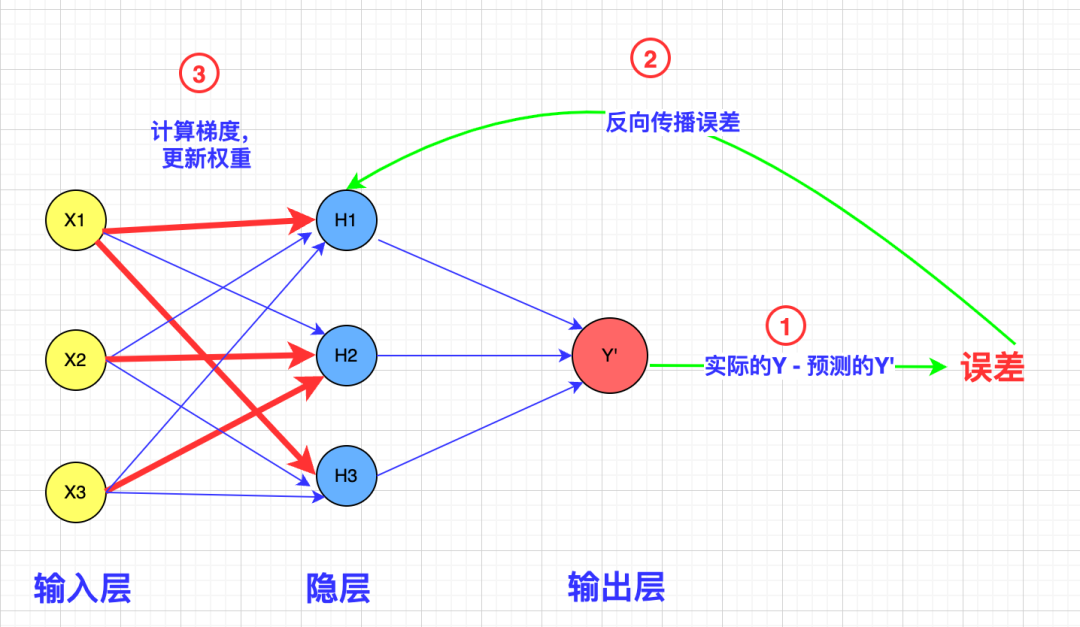
如果权重越大,误差就越大,我们就能有效地降低神经元的敏感度。
如何让误差正比于权重呢?很简单,把权重的绝对值或平方(因为误差有正有负)加到误差上就可以了:
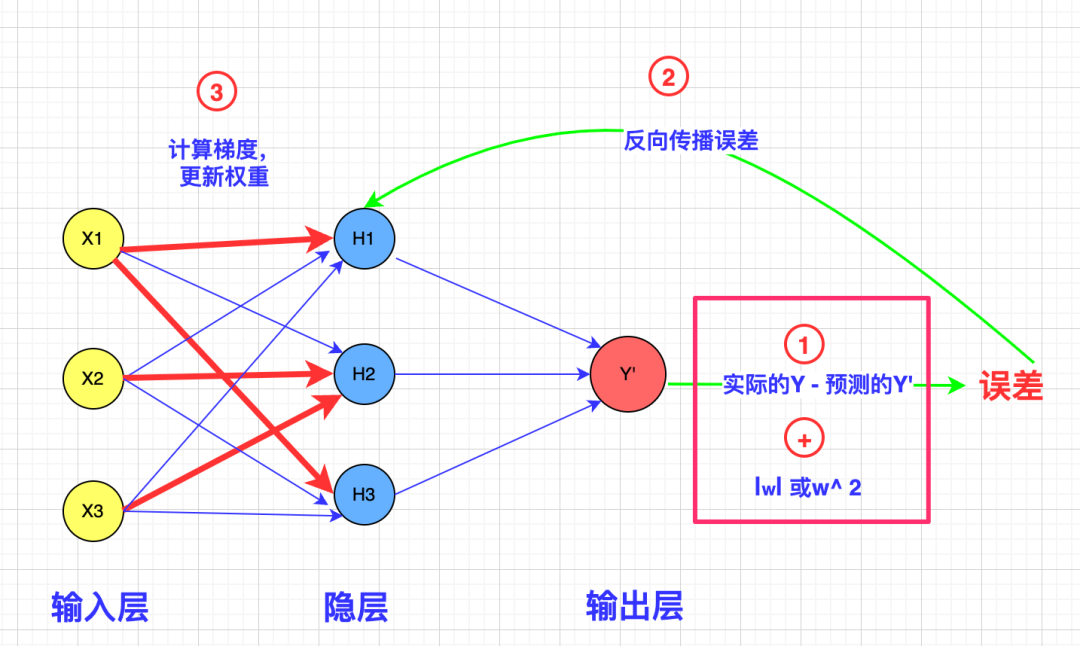
通过对过大权重值的惩罚,经过训练我们会得到类似这样的神经网络:
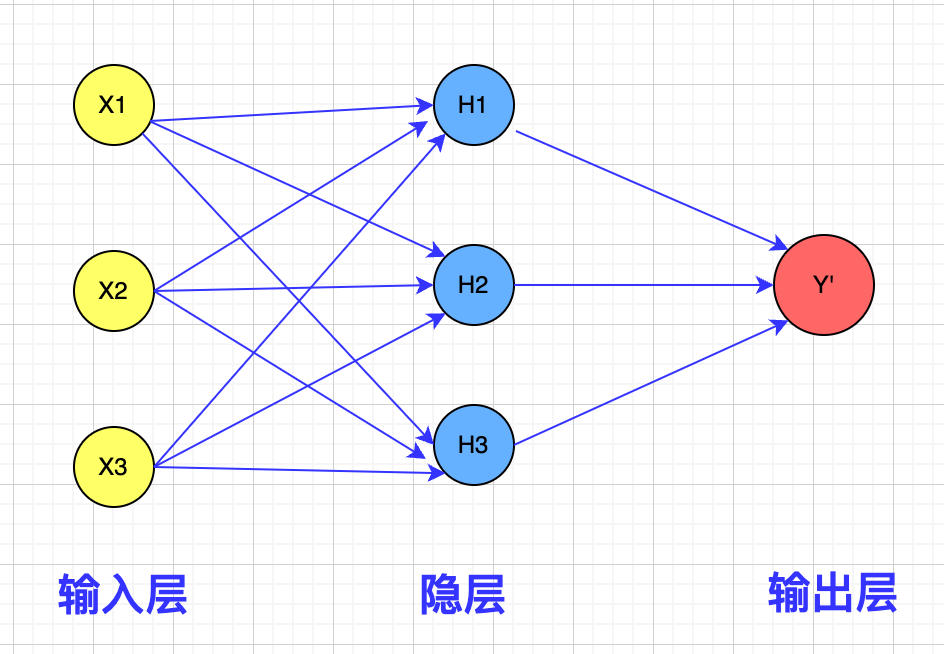
在神经网络中我们不再有过大的权重值,权重分布比较均匀,只有那些在数据中反复出现的规律才会被捕获,数据噪声被过滤。
【版權聲明】本文爲轉帖,原文鏈接如下,如有侵權,請聯繫我們,我們會及時刪除
原文鏈接:https://mp.weixin.qq.com/s/Xliq7LhcfQOFmSgDyfEDWA Tag: AI原理 神经网络
評論
相關內容