阿Q技术站
2024-03-21
157
0
0
0
0
在这个看似繁华却实际险象环生的时代,很多人都会感叹形势比想象的严峻许多。就在最近,看到一位小伙伴还想找以前的同事帮忙内推看有没有啥工作机会,结果问了一圈,除了一个已经跳到国企上岸了的,其余的竟然全都在家待业。。这些同事以前都是公司的骨干力量,尤其几个以前在一起做过完整项目,非常清楚他们的能力,结果现在都成这样,真是不知道说啥好了。 
图片来源于网络 阳春三月,又到了一年一次的金三银四阶段,从月初开始就看到各个互联网公司已经在陆陆续续开始今年的春招实习计划了,当然也有正式岗位,这些岗位对于一些考研没考上的同学也是一个很好的机会。对于一些人来讲,挑战还是有的,在经历了一个寒冬过后,开工第一天就有原地倒闭的公司,形式并没有那么好,但也没有想象的那么差。 也有好多小伙伴说到降薪,当然了,当盘子缩减的时候,人力就没有那么值钱了,所以降薪是正常操作。随着人工智能和自动化技术的飞速发展,一些工作岗位被机器取代的趋势愈发明显。再者,受到全球经济环境变化的影响,很多企业为了生存和发展,不得不采取裁员、缩减成本等措施。这两年看到降薪的企业一抓一大把,有多少人都是背着房贷车贷顶着压力。其实降薪和接受降薪都是无奈之举,对企业对人都是一种挑战。 
图片来源于网络 面对这样的大环境,我们个人可能会感到无力和焦虑。能做的就是保持乐观,坚定信念,不断提升自己的能力和素质,以更加积极的态度去适应和应对这个变化莫测的社会。虽然现在的情况充满挑战,但历史告诉我们,每一次危机都是转机的开始。保持积极的心态,不断学习和适应,以便能够在变化中找到自己的位置。或许,只有这样,才能在逆境中找到机遇,在困境中创造奇迹。 今天继续给大家分享我最近一直坚持的《图解面试经典算法系列》,前面已经完成了“双指针”和“链表”两个部分,现在到了二叉树部分,它也是数据结构中非常重要的一个模块,我和大家一起再重温一下校招面试比较高频的算法题——从前序与中序遍历序列构造二叉树。 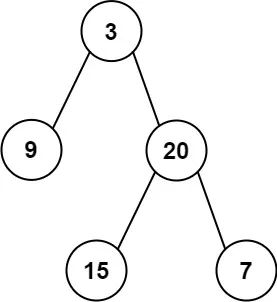
这道题是《图解面试经典算法系列》的第27道题,大家可以点下边的这个合集,基本上都是按顺序来的,觉得还行,顺便可以订阅一下。 往期精选: 校招生,农村人,拿到了大厂offer。一天工资是现在两个月生活费,我的人生第一次被彻底震撼了。。。
某大厂开发:工作5年,目前32岁,到手加公积金70w+一年,房贷已还清,过年回家被亲戚嘲讽还有3年就要下岗了。。。
腾讯QQ部门C++实习一面,回答上了85%,不知道是不是凉了。。。
腾讯QQ部门C++实习二面面经,一面只答了85%,没想到给二面了!!
最容易被背景调查识别出来的造假方式,你知道几种?
本文爲轉帖,原文鏈接如下,如有侵權,請聯繫我們,我們會及時刪除
原文鏈接:https://mp.weixin.qq.com/s/Qng3yVbvNbpE6dnECRkKRA Tag: 算法
網站名稱:真是被震惊到了,形势比想象的严峻多了。。。
網站地址:https://mp.weixin.qq.com/s/Qng3yVbvNbpE6dnECRkKRA
大家好,我是Q。在这个看似繁华却实际险象环生的时代,很多人都会感叹形势比想象的严峻许多。就在最近,看到一位小伙伴还想找以前的同事帮忙内推看有没有啥工作机会,结果问了一圈,除了一个已经跳到国企上岸了的,…
[SEO信息] [Alexa信息]
-->>直達網站
大家好,我是Q。


从前序与中序遍历序列构造二叉树
LeetCode.105
问题描述
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路
递归
构造二叉树的基本思路是利用先序遍历和中序遍历的特点。先序遍历的顺序是根节点、左子树、右子树;中序遍历的顺序是左子树、根节点、右子树。
首先,先序遍历的第一个元素一定是根节点的值。 然后,在中序遍历中找到这个根节点的位置,它左边的元素都是左子树的节点,右边的元素都是右子树的节点。 根据中序遍历中根节点的位置,可以得到左子树和右子树的节点数目,进而可以在先序遍历中找到左子树和右子树的分界点。 递归地构建左子树和右子树。
非递归
创建根节点并将其压入栈中。
初始化前序遍历索引
preIndex为 0,表示当前处理的是前序遍历的第一个元素(根节点)。循环执行以下步骤,直到栈为空:
a. 从栈中弹出一个节点作为当前节点。
b. 如果当前节点的值不等于中序遍历中的当前值(由
inIndex指示),则将当前节点的右子节点设置为前序遍历中的下一个值,并将右子节点压入栈中。c. 否则,更新
inIndex指示下一个中序遍历的值,并将当前节点的左子节点设置为前序遍历中的下一个值,然后将左子节点压入栈中。返回根节点。
图解
今天给大家画一个相对简单好理解的流程图。
3
/ \
9 20
/ \
15 7
preorder: [3, 9, 20, 15, 7]
inorder: [9, 3, 15, 20, 7]
1. 创建根节点 root = TreeNode(3)
2. 将 root 压入栈 s 中
3. preIndex = 1, inIndex = 0
4. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root
- root->val != inorder[0] (9)
- root->left = TreeNode(9)
- 将 root->left 压入栈 s 中
- preIndex = 2
5. preIndex = 2, inIndex = 0
6. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left (9)
- root->left->val != inorder[1] (3)
- root->left->left = TreeNode(20)
- 将 root->left->left 压入栈 s 中
- preIndex = 3
7. preIndex = 3, inIndex = 0
8. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left->left (20)
- root->left->left->val != inorder[2] (15)
- root->left->left->left = TreeNode(15)
- 将 root->left->left->left 压入栈 s 中
- preIndex = 4
9. preIndex = 4, inIndex = 0
10. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left->left->left (15)
- root->left->left->left->val != inorder[3] (20)
- root->left->left->left->right = TreeNode(7)
- 将 root->left->left->left->right 压入栈 s 中
- preIndex = 5
11. preIndex = 5, inIndex = 0
12. 进入循环,preIndex < preorder.size()
- preIndex == preorder.size(),跳出循环
13. 返回根节点 root
参考代码
C++
递归
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
unordered_map<int, int> index_map; // 用于存储中序遍历中节点值和索引的映射
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
// 构建中序遍历中节点值和索引的映射
for (int i = 0; i < inorder.size(); ++i) {
index_map[inorder[i]] = i;
}
return build(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
}
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pre_left, int pre_right, int in_left, int in_right) {
if (pre_left > pre_right || in_left > in_right) {
return nullptr; // 如果前序遍历或中序遍历的起始位置大于结束位置,返回空节点
}
int root_val = preorder[pre_left]; // 当前子树的根节点值
TreeNode* root = new TreeNode(root_val); // 创建当前子树的根节点
// 在中序遍历中找到根节点的位置
int index = index_map[root_val];
int left_size = index - in_left; // 左子树的节点数目
// 递归构建左子树和右子树
root->left = build(preorder, inorder, pre_left + 1, pre_left + left_size, in_left, index - 1);
root->right = build(preorder, inorder, pre_left + left_size + 1, pre_right, index + 1, in_right);
return root; // 返回当前子树的根节点
}
};
// 打印二叉树的先序遍历结果
void printPreorder(TreeNode* root) {
if (!root) {
return;
}
cout << root->val << " ";
printPreorder(root->left);
printPreorder(root->right);
}
int main() {
vector<int> preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
vector<int> inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution;
TreeNode* root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
cout << endl;
return 0;
}
非递归
#include <iostream>
#include <vector>
#include <stack>
#include <unordered_map>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.empty()) {
return nullptr; // 如果前序遍历序列为空,返回空指针
}
TreeNode* root = new TreeNode(preorder[0]); // 创建根节点
stack<TreeNode*> s; // 辅助栈,用于模拟递归过程
s.push(root); // 将根节点压入栈中
int preIndex = 1; // 前序遍历索引,从第二个元素开始
int inIndex = 0; // 中序遍历索引,从第一个元素开始
while (preIndex < preorder.size()) {
TreeNode* currNode = s.top(); // 获取栈顶节点作为当前节点
if (currNode->val != inorder[inIndex]) {
// 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode->left = new TreeNode(preorder[preIndex++]); // 创建左子节点
s.push(currNode->left); // 将左子节点压入栈中
} else {
// 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while (!s.empty() && s.top()->val == inorder[inIndex]) {
// 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = s.top();
s.pop();
++inIndex; // 更新中序遍历索引,指向下一个节点
}
currNode->right = new TreeNode(preorder[preIndex++]); // 创建右子节点
s.push(currNode->right); // 将右子节点压入栈中
}
}
return root; // 返回根节点
}
};
// 打印二叉树的先序遍历结果
void printPreorder(TreeNode* root) {
if (!root) {
return;
}
cout << root->val << " ";
printPreorder(root->left);
printPreorder(root->right);
}
int main() {
vector<int> preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
vector<int> inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution;
TreeNode* root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
cout << endl;
return 0;
}
Java
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
// 二叉树节点的定义
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0) {
return null; // 如果前序遍历序列为空,返回空节点
}
TreeNode root = new TreeNode(preorder[0]); // 创建根节点
Stack<TreeNode> stack = new Stack<>(); // 辅助栈,用于模拟递归过程
stack.push(root); // 将根节点压入栈中
int preIndex = 1; // 前序遍历索引,从第二个元素开始
int inIndex = 0; // 中序遍历索引,从第一个元素开始
while (preIndex < preorder.length) {
TreeNode currNode = stack.peek(); // 获取栈顶节点作为当前节点
if (currNode.val != inorder[inIndex]) {
// 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode.left = new TreeNode(preorder[preIndex++]); // 创建左子节点
stack.push(currNode.left); // 将左子节点压入栈中
} else {
// 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while (!stack.isEmpty() && stack.peek().val == inorder[inIndex]) {
// 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = stack.pop();
inIndex++; // 更新中序遍历索引,指向下一个节点
}
currNode.right = new TreeNode(preorder[preIndex++]); // 创建右子节点
stack.push(currNode.right); // 将右子节点压入栈中
}
}
return root; // 返回根节点
}
}
public class Main {
public static void main(String[] args) {
int[] preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
int[] inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution = new Solution();
TreeNode root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
System.out.println();
}
private static void printPreorder(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
printPreorder(root.left);
printPreorder(root.right);
}
}
Python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not preorder:
return None
root = TreeNode(preorder[0]) # 创建根节点
stack = [root] # 辅助栈,用于模拟递归过程
preIndex, inIndex = 1, 0 # 前序遍历索引从第二个元素开始,中序遍历索引从第一个元素开始
while preIndex < len(preorder):
currNode = stack[-1] # 获取栈顶节点作为当前节点
if currNode.val != inorder[inIndex]:
# 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode.left = TreeNode(preorder[preIndex]) # 创建左子节点
stack.append(currNode.left) # 将左子节点压入栈中
preIndex += 1 # 更新前序遍历索引
else:
# 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while stack and stack[-1].val == inorder[inIndex]:
# 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = stack.pop()
inIndex += 1 # 更新中序遍历索引
currNode.right = TreeNode(preorder[preIndex]) # 创建右子节点
stack.append(currNode.right) # 将右子节点压入栈中
preIndex += 1 # 更新前序遍历索引
return root # 返回根节点

ok,今天给大家的分享就到这儿, 快快订阅起来吧。
本文爲轉帖,原文鏈接如下,如有侵權,請聯繫我們,我們會及時刪除
原文鏈接:https://mp.weixin.qq.com/s/Qng3yVbvNbpE6dnECRkKRA Tag: 算法
評論
相關內容