这是本系列的第10篇文章，在这个系列中，我将尝试尽量用大白话的方式，来解释一些AI领域的基本概念，我相信不论AI背后的数学有多复杂，其基本思路一定是清晰的，可以用数学无关的方式讲清楚的。

近些年，AI领域的突破几乎都来自于深度学习，在深度学习的范式下，选择合适的神经网络架构(CNN, RNN, Transformer等)，甚至是基于一些预训练好的模型，只要有数据和算力，很多复杂的问题都能轻松解决，这极大地加速了AI的应用落地，但这种简化也有一定的代价，比如大量算力的消耗、模型的不可解释性等。

实际上，在具体应用场景中，很多问题用一些简单的机器学习方法就能取得不低于、甚至优于深度学习的效果，比如今天要介绍的决策树和随机森林就是一个这样的例子，我们将用一个Kaggle中的竞赛问题为例，和大家深入了解决策树和随机森林这一经典机器学习算法，我们将看到这一算法的优异效果、可观测和可解释性、以及极低的算力门槛要求。

要解决的问题

这是一个来自于Kaggle的竞赛：“Blue Book for Bulldozers”，其目标是给出一些重型设备的配置、型号、类型...等属性，以及这些设备的历史拍卖价格，通过这些数据来训练一个模型，然后再用这个模型在未来预测设备在拍卖中的价格，预测准确率最高的模型赢得竞赛的冠军。

虽然这只是一个Kaggle的竞赛，但在我们的实际工作中，常常碰到的预测销量、预测库存、预测价格等问题都和它非常类似，今天我们就来看看用朴素的决策树和随机森林如何简单高效地解决这类问题。

什么是决策树

顾名思义，决策树实际就是通过一些问题，层层递进、逐步缩小决策范围、得到最终决策的过程，下图就是一个例子：

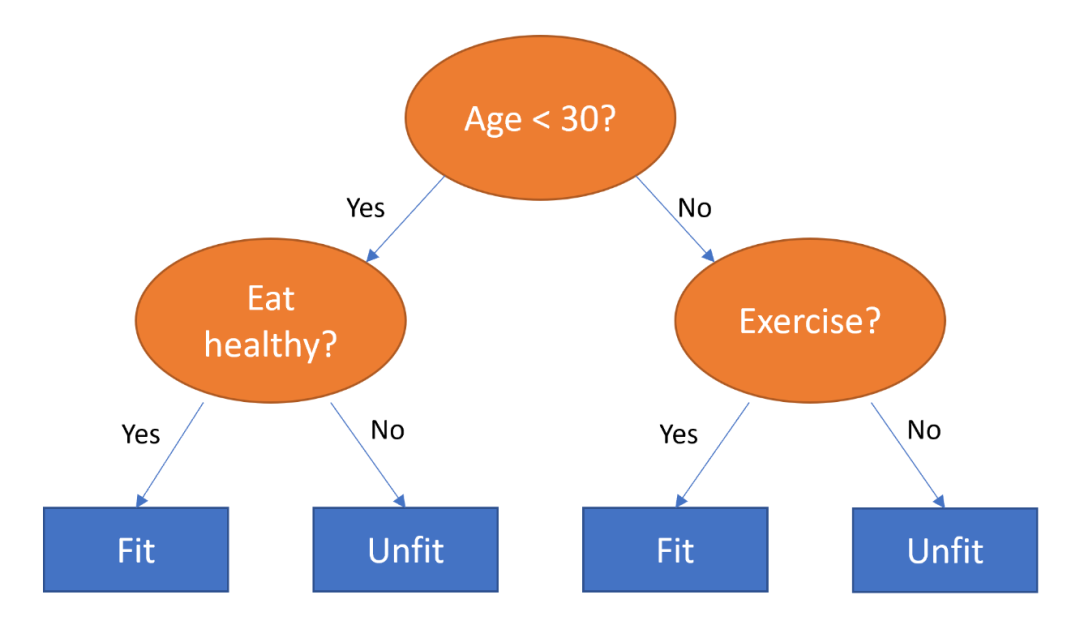
比如我们要预测一个人身体是否健康，就可以首先用年龄作为一个关键问题，如果这个人年龄小于30岁，那么就主要关注其饮食是否健康，只要饮食健康，则这个人身体应该就会比较健康，反之则可能不健康；而如果这个人年纪大于30岁，那么是否锻炼就是关键因素了，保持锻炼的人应该会比较健康，反之则可能不健康。

可以看到决策树的概念很简单也很好理解，有的同学可能会说，如果有了这棵树，解决问题确实很简单，但问题是我们如何构建这棵树呢？一个实际问题往往有几十上百个影响因素，到底哪个因素应该是决策树的根节点、哪个因素应该是中间节点呢？

如何构建一棵决策树

要回答上述问题，借助计算机，通过一套简单机械的步骤就能帮我们找到一棵决策树，其具体过程如下：

1. 遍历问题所有属性的所有可能取值
   
2. 对一条训练数据，看这条数据该属性的值是大于还是小于当前取值(对于类似大、中、小这种类别属性，则看这条数据该属性是否等于当前取值)，通过这个方式把所有的训练数据分为两组
3. 对这两组数据分别取目标值(如拍卖价格)的平均值，然后看这个平均值和该组数据中每条数据实际目标值的误差
   

当我们遍历完所有属性的所有可能取值后，我们就遍历了所有可能的分组，此时我们取误差最小的分组方式作为决策树的根节点，此后我们对根节点下的两组数据，重复上述过程，就可以得到决策树的第二层节点，这样不断递归，直到达到了预定的结束条件(如达到了预定层数、或者叶节点里的数据少于预定的阀值等)。

用决策树来预测设备的拍卖价格

了解了决策树的原理和构建过程后，现在让我们来试着解决上面提到的Kaggle上预测设备拍卖价格的问题，作为一个演示，让我们把构建决策树的结束条件设置为最多有4个叶节点，我们可以得到如下决策树：

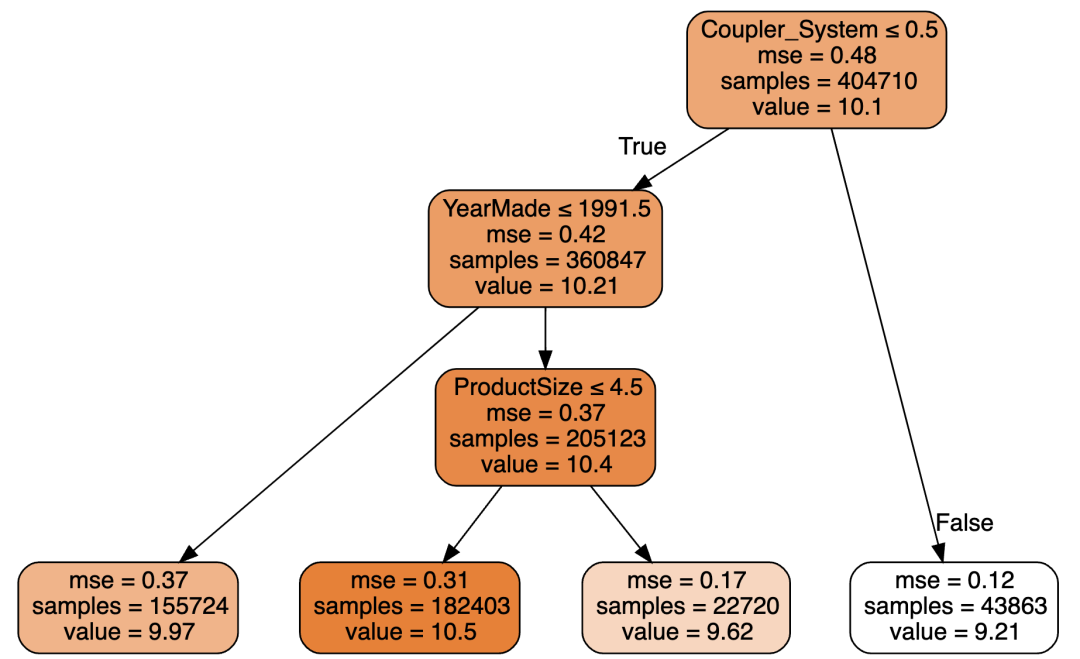
图中每个节点的第一行是分组的判断条件，第二行是误差平方的均值(Mean Square Error, 取平方的原因是误差可能为正、可能为负，直接取均值会正负相抵，取平方后则都成为正数避免了正负相抵的问题)，第三行是该节点下总共有多少条数据，第四行则是价格的均值。叶节点因为不再需要继续分组，所以没有分组条件。

有了这棵决策树，给我们一个新的设备，我们根据决策树各节点的判断条件，可以把这个新的设备归类到某个叶结点，那么这个叶结点的价格均值就是我们对这个新设备拍卖价格的预测。

可以看到越是靠下的节点，其误差也越小，这也就是决策树层层递进、逐步缩小问题范围、最终解决问题这一思路的体现。

决策树的每个节点都有一个误差的衡量值MSE，那么整个决策树的误差该如何衡量呢？其实其计算过程和计算单个节点MSE的过程是一样的，就是遍历所有的样本数据，计算实际价格和预测价格的差取平方，加总后除以总的样本数得到的均值。

决策树的误差是不是越小越好？

如上所述，一棵决策树的误差用MSE来衡量，那么这个误差最小可以达到多少呢？答案是0。

如果我们在构建决策树时持续递归，那么最后我们可以得到一棵每个叶节点上都只有1条数据的决策树，每条训练数据都会落到一个叶节点上，这样一棵决策树可以100%准确地对训练数据进行预测，换个角度，相当于是这棵决策树记住了每一条训练数据。

显然，这是一种过拟合，那么在实践中，如何判断是否存在过拟合呢？一般，在训练决策树前，我们需要先预留出一部分数据(一般是20%)不参与训练，当训练完成后，我们再用这些训练时没见过的验证数据来衡量决策树的实际效果。如果我们发现训练数据的MSE越来越小，而验证数据的MSE先变小然后又开始变大，那么就说明我们出现了过拟合问题。

防止过拟合的一个常见手段是避免叶节点包含的数据太少，在构建决策树时，我们可以把叶节点至少包含多少数据作为一个结束条件，如果我们发现出现了过拟合，就可以试着增加这个阀值，重新训练我们的决策树。

在上述Kaggle竞赛预测设备拍卖价格的问题上，当我们把结束递归的条件设置为叶结点至少要包含25条数据时，我们的决策树，其训练误差为0.24854，验证误差为0.3234。(在本系列的上一篇文章，在用大白话介绍的同时，我还试着增加了代码来说明问题，发现效果适得其反，因此这里就略去了实际代码，集中说明决策树的工作原理).

我们的验证误差0.323396这个成绩如何呢？Kaggle上竞赛第一名的成绩是0.22909，我们的成绩还有不小差距。

用集体智慧来提高成绩

相信很多人都看过下面这个神奇的故事：

1906年，心理学家弗朗西斯•高尔顿来到一个集市，目睹了一场有800人参加的猜重量比赛：猜一头公牛的重量，他收集了所有人的测算并计算出平均值，得出的结果是1208磅。令高尔顿惊讶的是，这与这头牛的真正重量（1198磅）相差只有10磅，误差不到1%！

这个故事讲的是集体的智慧，应用到我们Kaggle竞赛，我们使用集体智慧的一个方法就是“随机森林”。

随机森林的想法也很简单，既然一棵决策树的预测不够好，那么我们就训练多棵决策树，然后取这些决策树预测值的均值作为最终的输出。

那么怎么训练多棵决策树呢？也很简单，就是从全量的训练数据集中，随机取一个子集，然后用这个子集来训练得到一棵决策树，重复这一过程就可以得到多棵决策树了。

更进一步，除了可以随机取一部分数据来做训练数据外，我们还可以随机取部分属性来训练决策树，既然是集体智慧，那么具体每棵决策树就不一定需要特别优秀了。

这一策略的效果如何？当我们的随机森林有40棵决策树，属性使用率为50%时，我们的训练误差和验证误差分别为：0.17092, 0.23398，可以看到验证误差0.23398和最好成绩0.22909已经比较接近了，集体智慧真是神奇。(Kaggle上的成绩是用不公开的测试数据来验证得到的，这里的直接比较并不准确，但也可以作为一个不错的参考)

既然40棵决策树效果不错，是不是增加更多的决策树可以进一步提升效果呢？下图是森林中决策树数量的效果，可以看到当决策树的数量超过30棵后，继续增加决策树，获得的收益就不大了。

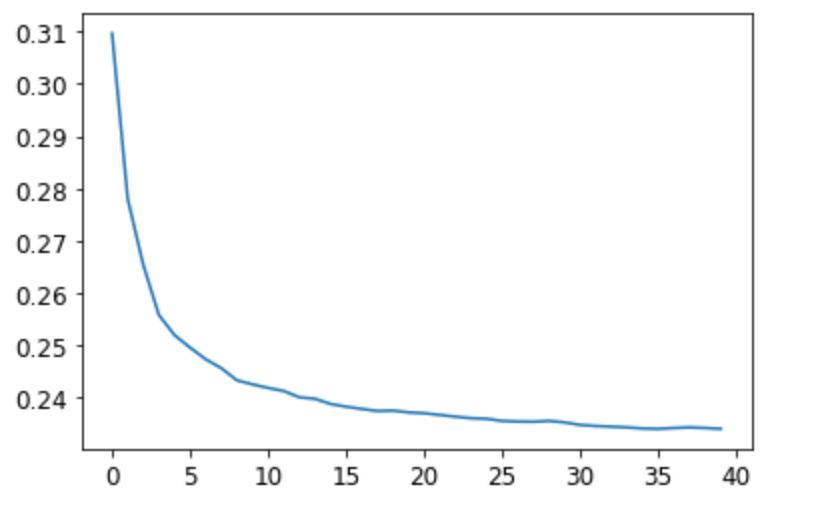
那么使用多少比例的属性效果比较好呢？下图是来自sklearn的一个研究：

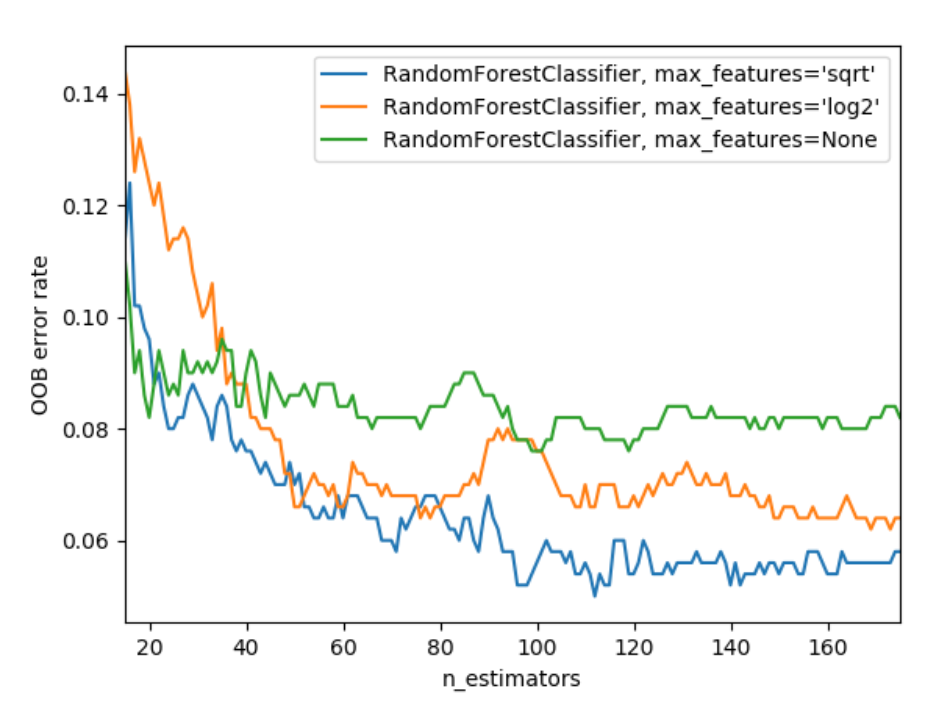
横轴是森林中决策树的数量，纵轴是OOB错误率(另一种衡量模型效果的指标)，绿色的线使用全量属性，橙色的线是使用log2数量的属性，而蓝色的则取平方根数量的属性，可以看到用更少的属性，可以一定程度提升模型效果，但起关键作用的还是决策树的数量。

抓住主要矛盾

从上面随机森林的分析，我们可以得到一个启发，既然只使用部分属性就可以训练决策树，那么是不是我们可以首先从全量属性中丢弃一些不重要的属性，然后再来构建随机森林呢？

借助fast.ai的API，我们可以得到下图：

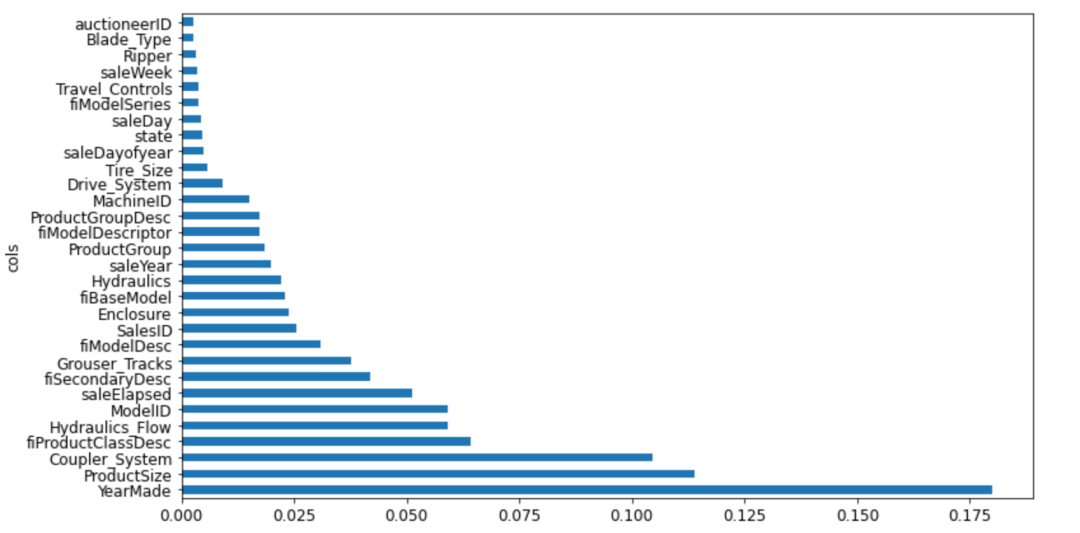
横轴是重要性，纵轴是重要性排名前30的设备属性，可以看到，即使在前30个属性中，也有很多属性影响不大，实际上，重要性大于0.005只有21个，如果我们只用这21个属性来训练我们的随机森林，我们的训练误差是0.1812，而验证误差是,0.23033， 可以看到训练误差略有上升，而验证误差则略有改善。

除了可以忽略非关键因素外，在我们使用的决策因素中，有很多因素是强相关的，再次借助fast.ai的API，我们可以得到下图：

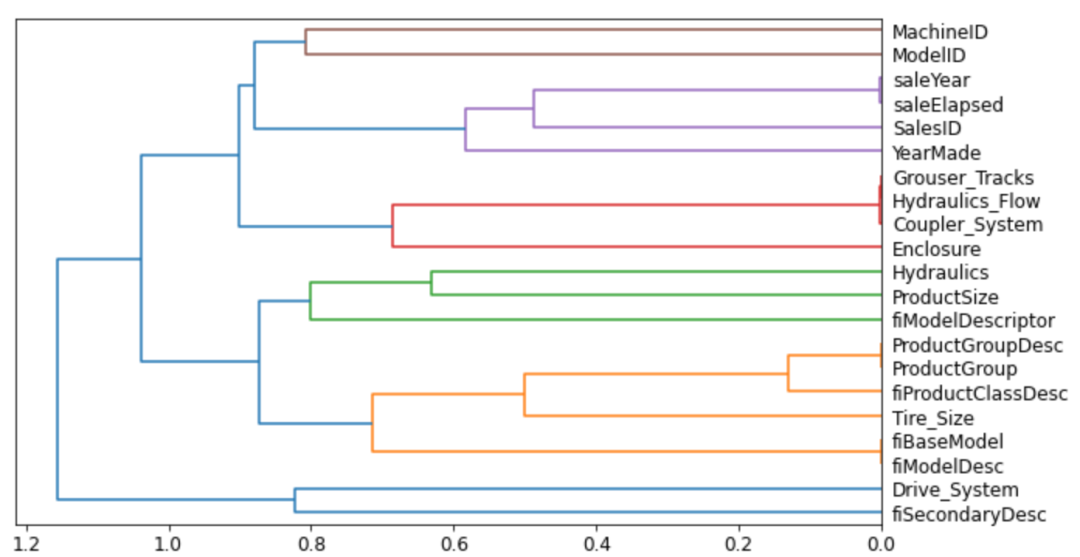
这是一棵横着放的树，越是靠右关联的节点其相关性越高，可以看到比如ProductGroup和ProductGroupDesc就强相关，saleYear和saleElapsed、fiModelDesc 和 fiBaseModel、Hydraulics_Flow和Grouser_Tracks也是如此，让我们试着丢弃saleYear，ProductGroupDesc， fiBaseModel， Grouser_Tracks看看效果，重新训练随机森林，我们的训练误差和验证误差为：0.183426, 0.231894，数据略有恶化，但并不明显。

按照奥卡姆剃刀原理，如非必要，勿增实体，通过减少不必要的属性，我们可以很大地减少训练过程的计算量，模型也会更加稳定，而模型的效果却不会有明显的变化。

决策树的可解释性

决策树的一个显著优势就是其可解释性，上面我们对关键属性、相关属性的分析，就是决策树可解释性的一个体现。

可解释性的另一个应用是数据洞察，即使我们用决策树、随机森林能比较好地进行预测，很多时候，我们也想知道为什么。

比如在“抓住主要矛盾”部分，我们能看到"YearMade"(制造年份)这个属性对价格预测最为重要，如果我们想看看该属性到底如何影响价格的话，一个直接的想法是，按照YearMade这个属性的取值，逐年看各年份设备销售价格的均值，看看能不能有些有趣的发现。

上述这个方法有一个缺点，那就是影响价格的因素有很多，我们按YearMade逐年取价格均值，在其它因素的干扰下，有可能得不到什么结论，或者即使能有一些发现，也并不可靠容易被干扰。

为了解决这一问题，有一种叫做“Partial Dependence”的技术，假设"YearMade"的可能取值为1950，1951，...，2020，2021，我们保持"YearMade"之外所有的其它属性值不变，然后把所有设备的"YearMade"值全部替换为1950，然后让模型预测这些设备的价格取均值，接着用1951作为所有设备的"YearMade"值，用模型预测取均值，重复这一过程直到尝试了YearMade的所有可能取值，这样我们就可以得到下图：

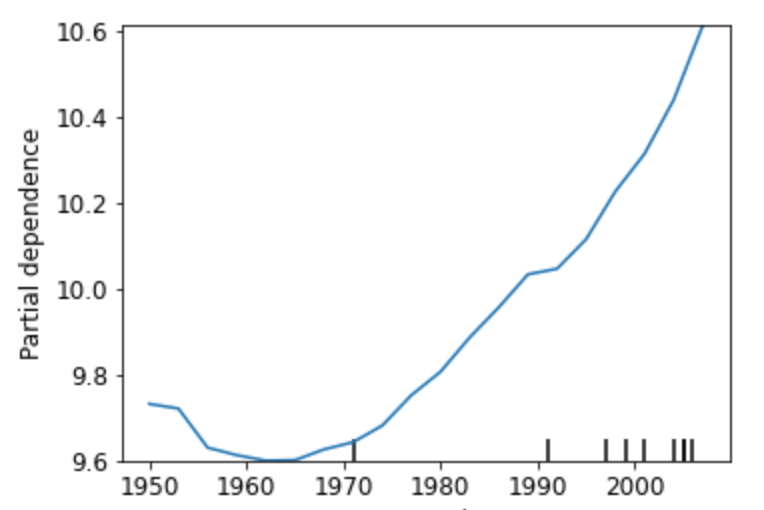
可以看到从1965年后，YearMade(制造年份)和价格几乎是线性相关的，制造年份越久价格越低，年份越近价格越高。

这里我们能得到什么关键结论？答案是对于这些重型设备，设备的折旧对设备的价格有决定性的影响，结合我们的常识，我们知道重型设备往往用来进行一些大型作业，设备很容易损耗，所以折旧确实是人们的首要关注点。

类似地，我们还可以用同样的技术对第二重要的因素"ProductSize"进行分析，这里就不再展开了。

数据陷阱

利用决策树的可解释性对问题的关键因素进行分析，不但能帮我们得到一些业务洞察，有时也能帮我们发现一些隐藏在数据中的陷阱。

下面是一个非常有意思的故事，在大学里，每年都有很多研究人员提交很多项目以申请研究经费，有人用随机森林做了一个模型，用来预测什么样的项目比较容易获得经费，用类似我们上面介绍的分析方法，他发现了两个有意思的现象：

1. 看起来毫无意义的项目编号居然对预测项目能否获得经费起着关键作用

2. 周末和年末提交的项目相对更容易获得经费

   
   

这两个现象非常违背常识，经过深入调查才发现，在该大学的系统中，一个项目提交时是没有编号的，只有该项目被批准经费后，才会被赋予一个编号，有了这个洞察后，显然项目编号这个属性不应该被模型用来做预测。

深入调查的另一个发现是，审批人员往往会在周末、年末的时候加班处理堆积的项目申请，系统会用项目的实际处理时间作为提交时间，有了这个洞察后，我们就知道项目实际的提交时间其实对是否获得经费没有影响。

这个故事是现实世界的真实写照，我们在处理实际业务的时候，我们拿到的数据可能是不完全的、也有可能是受到污染的、还有可能数据的真实含义和字面含义是完全不同的，更重要的是，即使数据本身是干净的，如果没有对业务的深入理解，我们对数据的解读也可能是错误的，这也就是很多AI领域的老手经常说"Know How"很重要的原因。

决策树的局限

决策树有着简单易懂可解释等优点，但它也有着一些固有的缺陷。

下图是一个简单线性函数加入一定噪音后的40个采样数据：

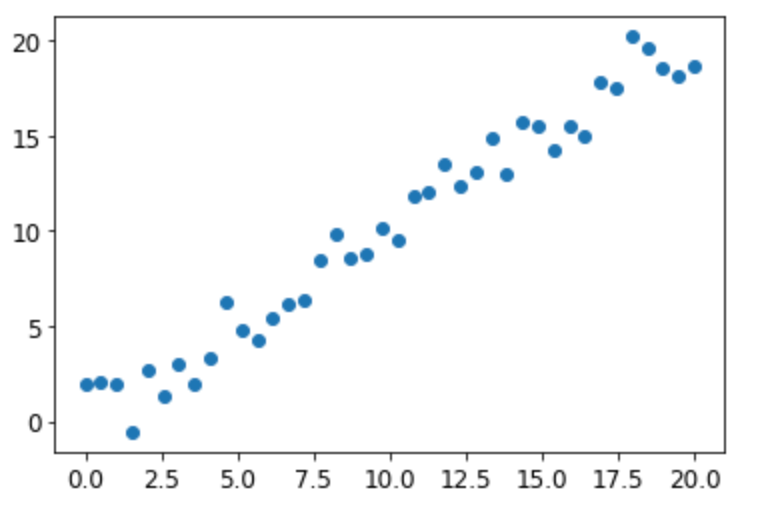
我们用前30个数据点做训练数据，训练一个随机森林，然后用后10个数据点做验证数据，来看看我们模型的效果：

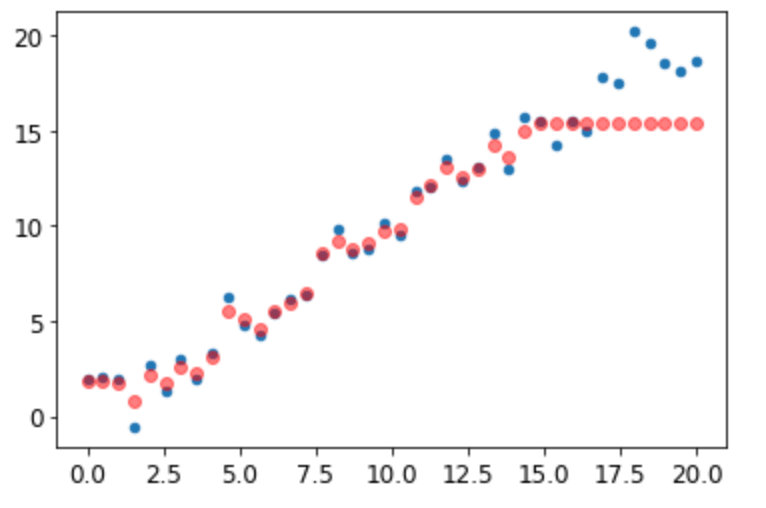
图中红色的点是模型的预测值，可以看到模型在训练集上表现很好，但是在验证集上给出的值却显著偏低，这是为什么呢？

回想一下决策树的定义，我们知道，决策树总是先把输入数据划分到某个叶节点，然后取叶节点的均值作为输出。这里的问题是，我们的数据有一个明显的趋势，当我们用一些历史数据的均值来预测趋势数据的时候，自然我们的预测总是会偏低。

实际上，这个问题并不仅仅局限于趋势数据，因为决策树是用历史的均值来预测未来，所以决策树无法有效外推没见过的数据分布或数据类型，当未来无法用历史表达的时候，决策树就会出现系统性的偏差。

那么，这类问题怎么解决呢？在大白话说AI：写给程序员的神经网络指南，无需数学、轻松理解、深度剖析中，我们介绍了神经网络，其工作方式可以看作是用一种函数来拟合训练数据，当未来无法用历史表达，但遵循某种规律的时候，深度学习/神经网络可能就是一个有效的解法。