我们在上篇文章中介绍了RNN背后的基本思路，然后动手实现了一个自己的RNN语言模型，接着对其进行了优化，在优化过程中，随着神经网络的变得越来越深，我们的模型出现了过拟合现象，同时模型的性能还出现了退步，在本文中，我们将一起了解RNN架构的缺陷，以及RNN的强化版LSTM的解法，最后我们还将一起动手实现一个LSTM架构的语言模型。

RNN的缺陷

首先，我们先来回顾一下RNN的基本架构：

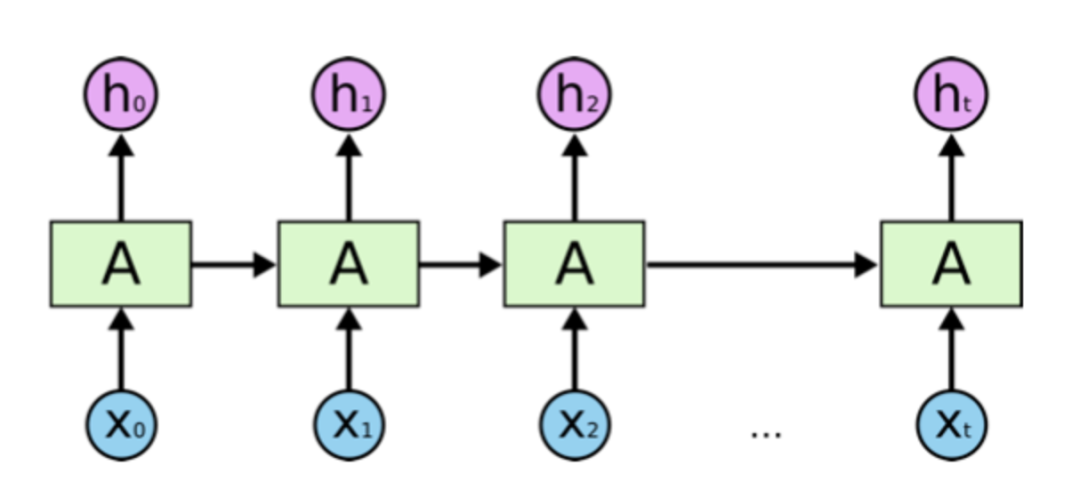
X0, X1, ... Xt是输入的文本序列，中间的方框是RNN节点，连接RNN节点的是从左到右不断传递的Hidden State(可以理解为关键上下文信息)，每个RNN节点接收来自前面节点的Hidden State，以及当前位置上的单词，并通过这两个输入计算一个新的Hidden State作为输出，并向下传递。

可以看到，这里的关键是图中的RNN节点，我们把这些RNN节点想像成一个个处理信息的人，然后重新画一下这个图：

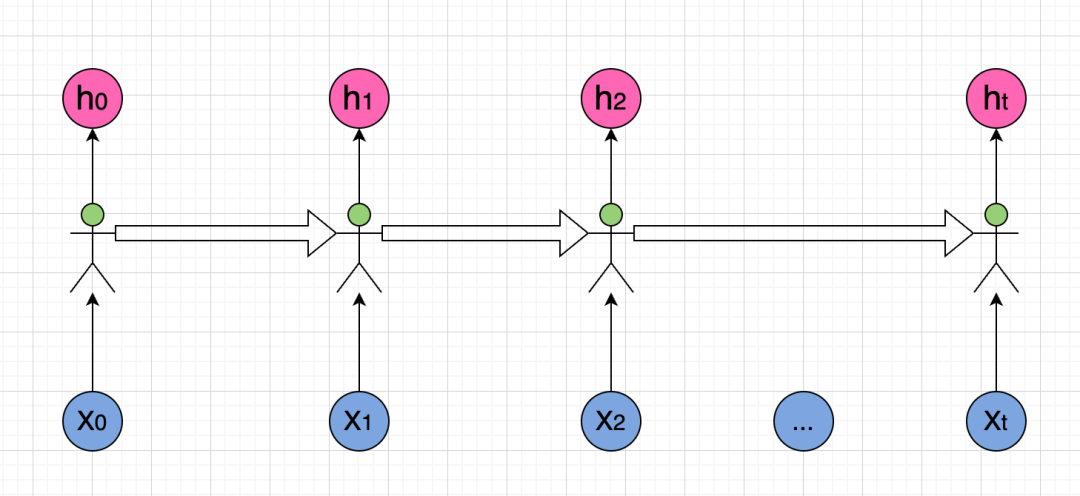
看到这个图，不知道大家有没有联想到什么？如果没有的话，我们再来看看这个图：

RNN网络是不是和传话游戏很像？

实际上RNN网络有着和传话游戏一样的问题，那就是Hidden State(关键信息)在RNN链条上不断向下传递时，每经过一个节点都会有一定的信息丢失，当RNN链条比较长的时候，文本序列开始处的信息传递到链条末尾时已经所剩无几了，简单来说，RNN只有短期记忆。

这就是为什么在上文中，当优化模型时，随着模型的深度(也就是RNN链条的长度)变得越来越深，模型短期记忆症的影响也变得越来越大，所以我们的模型性能并没有得到提升。

当然任何类比的解释都是不严谨的，从数学角度看，假设第t个RNN节点对Hidden State的加工用函数ft(xt, ht-1)来表示，由于前一个RNN节点的输出是后一个RNN节点的输入，当训练模型求导计算梯度的时候，如果用f'表示f的导数，那么我们在第t步计算导数就会出现f't * f't-1*f't-2...f'0这种连乘的情况，此时，如果我们的权重矩阵取值比较小，连乘之后结果会迅速趋近于0，这就会出现所谓梯度消失的问题，而如果权重矩阵取值比较大的时候，连乘之后结果会迅速趋近于无穷，这就会出现所谓梯度爆炸的问题。

数学推导总是枯燥，但我觉得传话游戏这个类比能很好地帮我们理解RNN的缺点。

如何让RNN具有长期记忆

如何解决RNN的短期记忆症呢？最直接的想法就是给RNN增加长期记忆，那么具体又该如何实现呢？

让我们还是回到传话游戏，假设我们在游戏中增加一个记事本，游戏中的每个人除了通过传话这个方式传递信息外，还可以在记事本上把关键信息记录下来，下一个人除了接收到上一个人传过来的话之外，还可以看到记事本，并把自己认为关键的信息添加到记事本上，这样就可以极大地减少信息丢失了，我们画个图来展示一下：

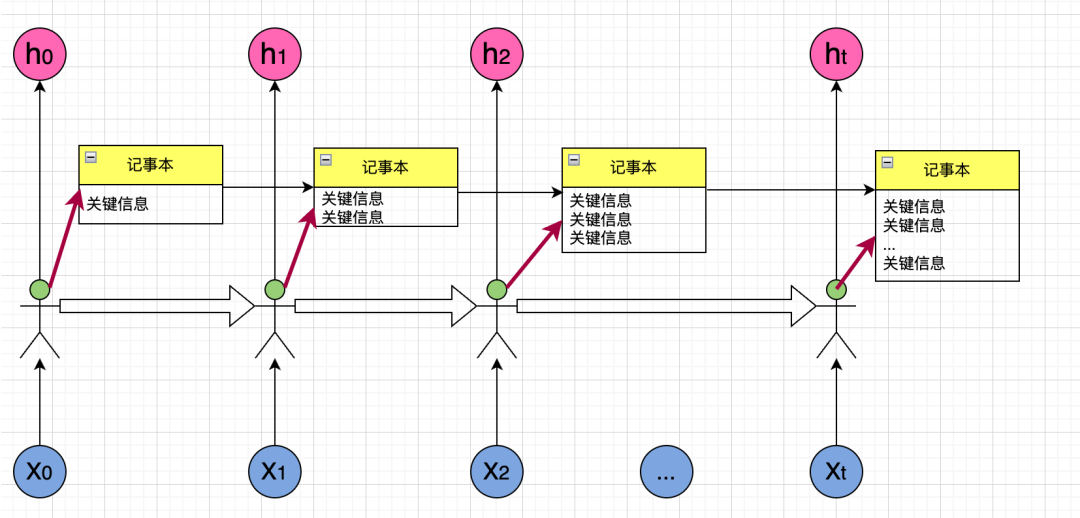
仔细观察，我们会发现记事本上的内容会越来越多，过多的内容并不是好事，比如"I grown up in China, so I an speak __"，最后一个单词是speak，如果我们知道句子前面的关键信息是"China"，那么预测缺少的单词就很容易，但如果这里的关键信息除了"China"，还有"I", "grown"等，这反而会干扰我们做出正确的预测。所以，在上图中，每个人除了向记事本中添加信息外，还需要把不再重要的信息删除：

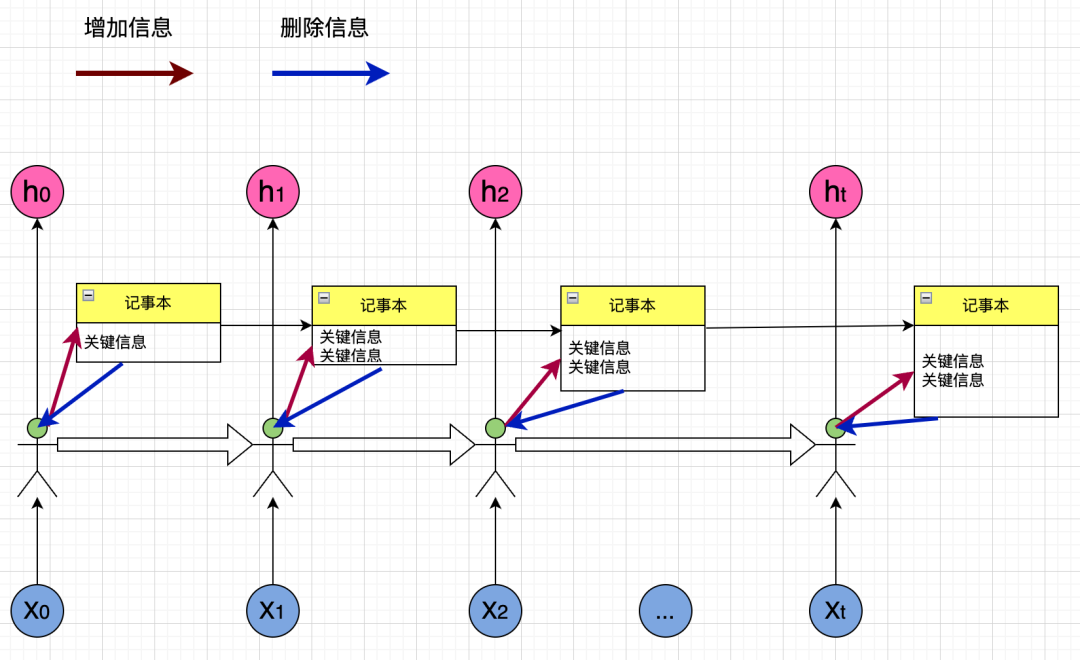
现在这个传话游戏既有短期记忆也有长期记忆了，这个RNN的变种就叫做LSTM(Long Short-Term Memory)，我们来看看一个真正LSTM神经网络的架构：

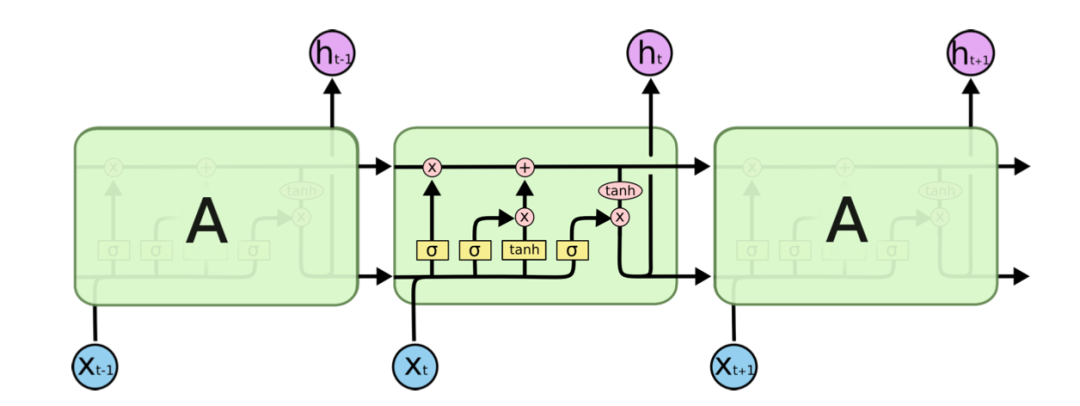
看来有些复杂，我们来给它做些标记：

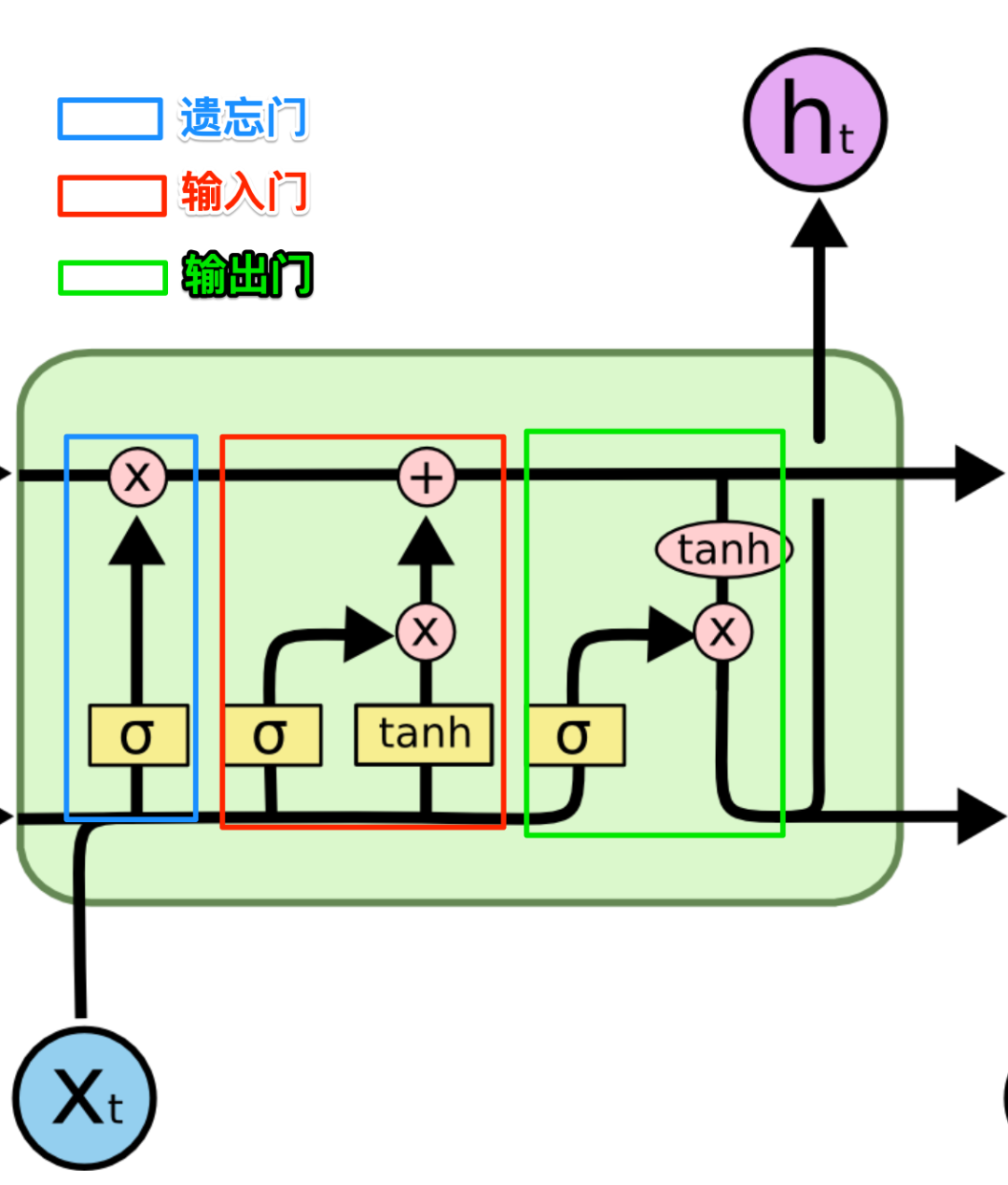
图中上方那条水平的箭头就是我们的记事本，在LSTM常用C表示，蓝色的框在LSTM中叫做遗忘门，负责从记事本中删除不再重要的信息，红色的框在LSTM中叫输入门，负责向记事本添加信息，绿色的框叫做输出门，负责向外输出LSTM节点的计算结果，现在让我们再来仔细看看这几个门。

首先是遗忘门：

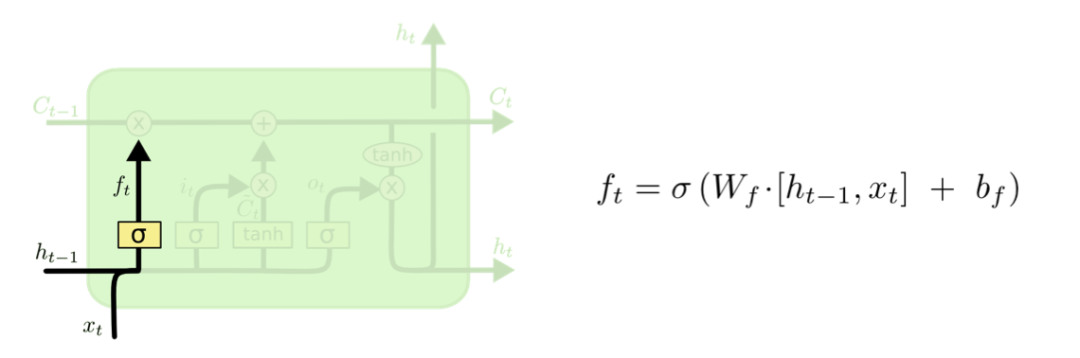
遗忘门把之前的Hidden State ht-1以及当前步的输入xt作为输入，合并成一个大的向量，乘以一个权重矩阵，然后用非线性函数sigmoid把结果转换为0到1之间的值以备后用，这个结果叫做遗忘器。

然后看看输入门：

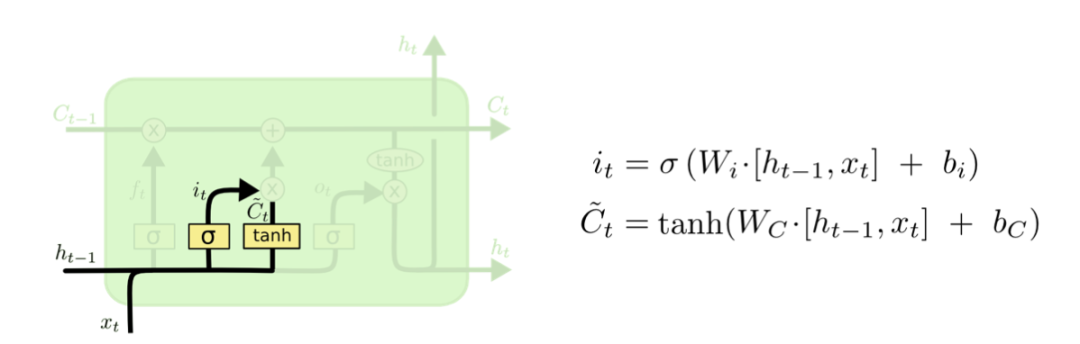
输入门有两个操作：

• 首先还是把之前的ht-1以及当前步的xt合并成一个大的向量，然后乘以一个权重矩阵，接着用非线性函数tanh把结果转换为-1到1之间的值，这个结果是要添加到记事本中的备选信息
• 同时输入门还是用ht-1及xt合并成的大向量乘以另一个权重矩阵，并用sigmoid处理得到一个选择器以备后用

然后我们来更新记事本：

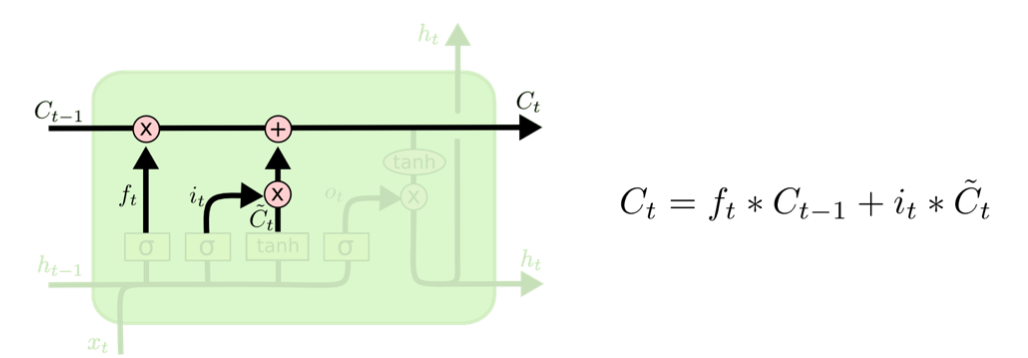
首先用遗忘器乘以原来的记事本以删除记事本中不再重要的信息:

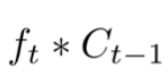
接着再用选择器乘以要添加的备选内容得到真正要添加的内容:

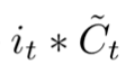
上面两步的结果相加就完成了记事本的更新操作。

最后是输出门：

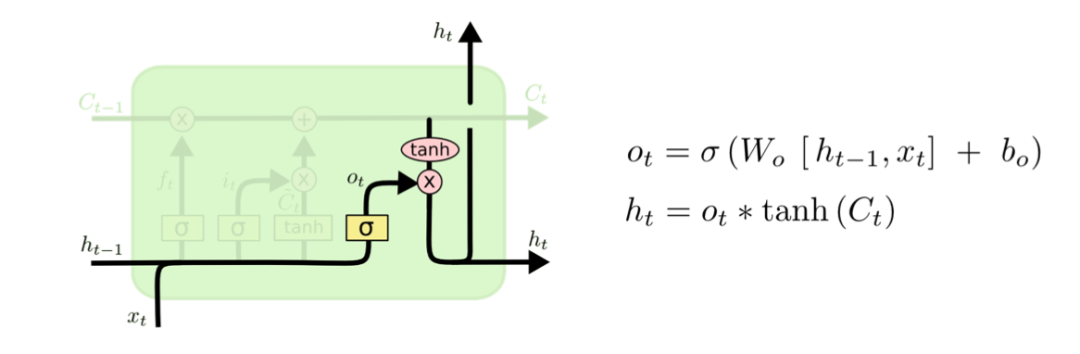
输出门首先还是把之前的ht-1以及当前步的xt合并成一个大的向量，接着乘以一个权重，然后用非线性函数sigmoid处理后作为一个选择器，然后我们把记事本用非线性函数tanh处理，最后和选择器相乘得到最后的结果输出。

这就是遗忘门、输入门、输出门以及记事本的详细工作过程。

用代码实现一个LSTM

明白了LSTM的工作原理后，代码实现是比较简单的，下面的实现基本就是上述工作过程的代码描述：

我们在上一篇文章中实现了基础版的RNN模型(建议阅读基础版RNN的实现以更好地理解下面的代码)，现在只需要把基础版中的隐层换成上面刚刚实现的LSTM Cell就可以了：

接下来让我们训练模型看看效果，这里我们复用了基础版RNN实现中定义的数据加载器dls3和损失函数loss_func:

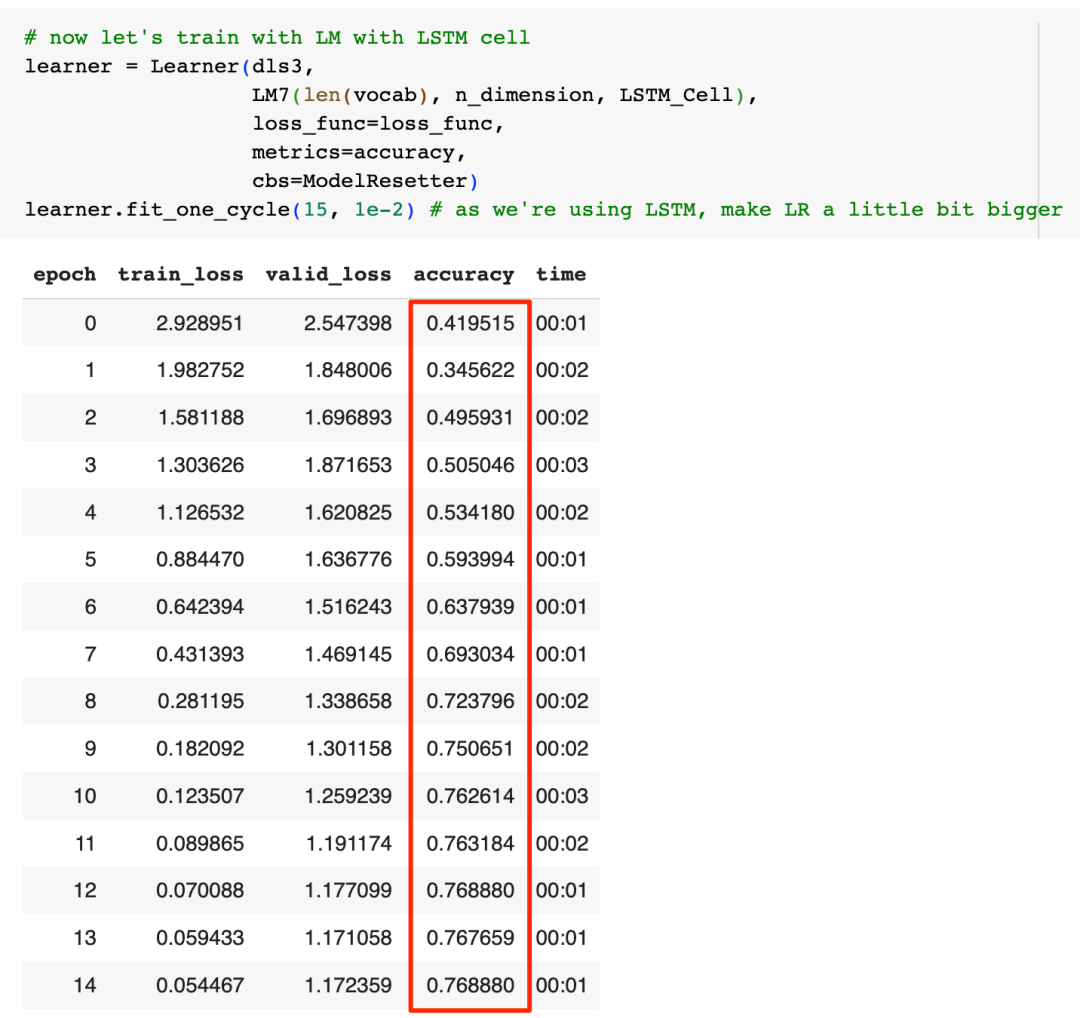
可以看到在拥有了长期记忆后，模型的表现从基础版的60%左右直接提升到了76.89%，同时并没有发生过拟合现象，LSTM的效果非常好。

改进我们的LSTM模型性能

仔细看LSTM的工作过程，我们能看到“把之前的Hidden State ht-1以及当前步的xt合并成一个大的向量，接着乘以一个权重”这样的操作进行了4次，因为这些操作都是矩阵乘法，所以我们可以把这些操作合并到一个大矩阵，用一次矩阵乘法完成这4个操作以提高性能，让我们来重构一下LSTM Cell的实现：

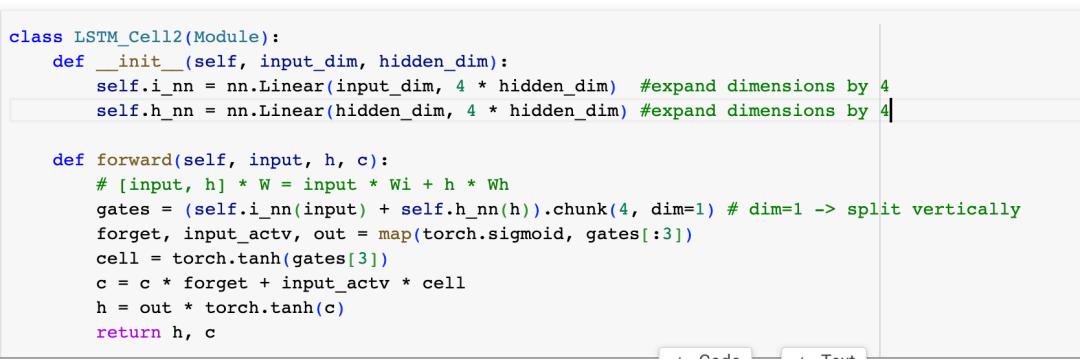
然后用新的LSTM Cell的实现来重新训练模型：

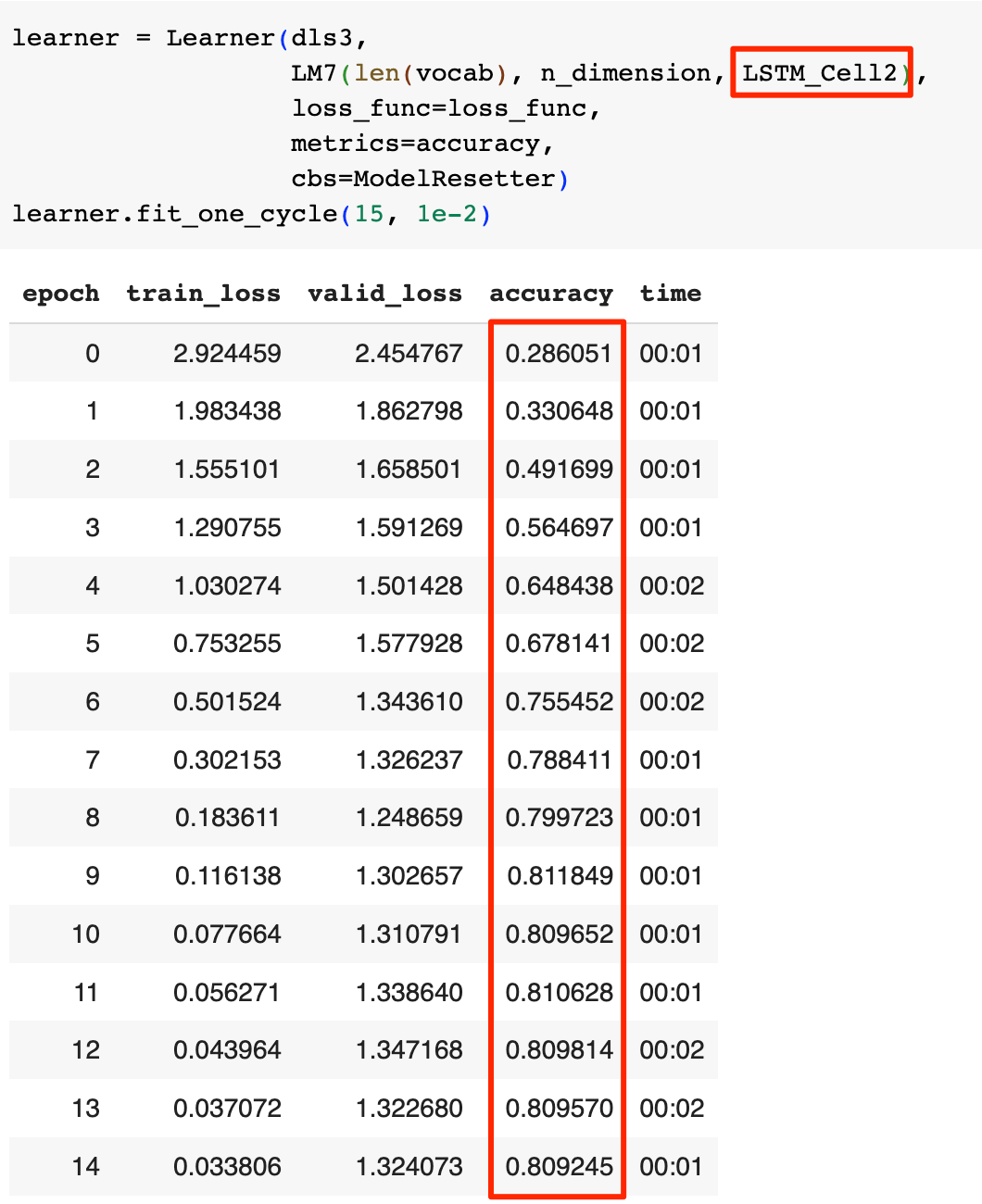
在模型性能提高的同时，准确率进一步提升到了80%左右，同时一样没有观察到过拟合现象。

在通过代码理解了LSTM的工作原理后，我们可以用PyTorch提供的LSTM类库来替换我们自己的手工实现。此外，如我们在介绍RNN基础版时提到的，作为一个常见的策略，增加模型的层数，往往可以提升模型的表现，因为没有观察到过拟合现象，所以可以放心地增加LSTM的层数，让我们再次重构模型：

然后我们用一个两层的LSTM再次训练模型看看效果：

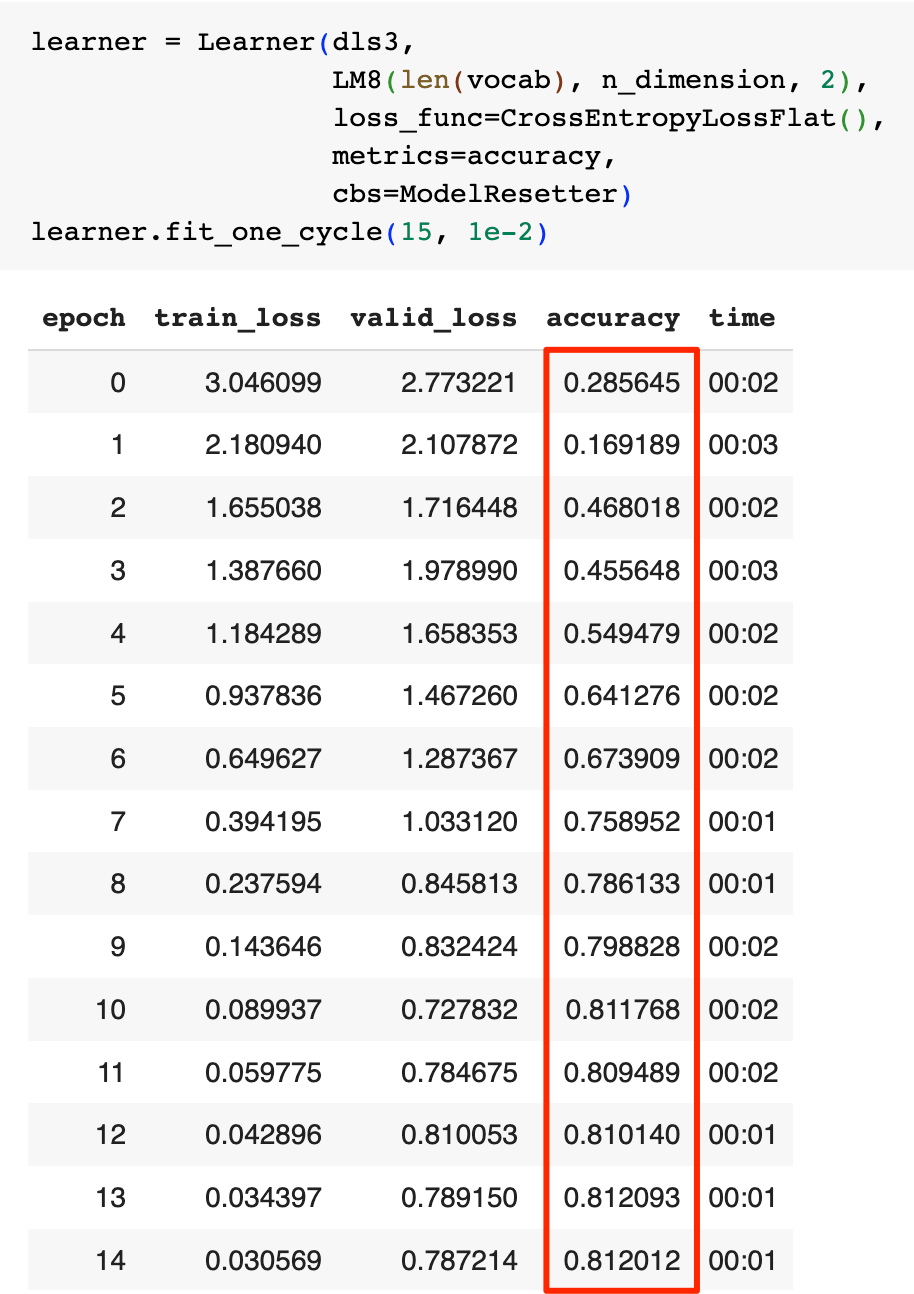
这次模型的性能仅有小幅提升达到了81.2%，但valid_loss收敛得很快，说明模型的学习能力还是有了提升。

应用常见的优化技巧

最后，训练神经网络有一些常见的优化技巧，我们可以应用这些技巧来进一步提升模型性能，这里我们只做简单介绍，如果展开仔细介绍的话，不是一篇文章长度可以承载的。

第一个优化技巧是Dropout，简单说就是理论和实践都发现，在训练模型时，在神经网络的激活权重中，按一定比例随机挑选一些权重重置为0，模型的泛化能力会强，模型的表现会更好：

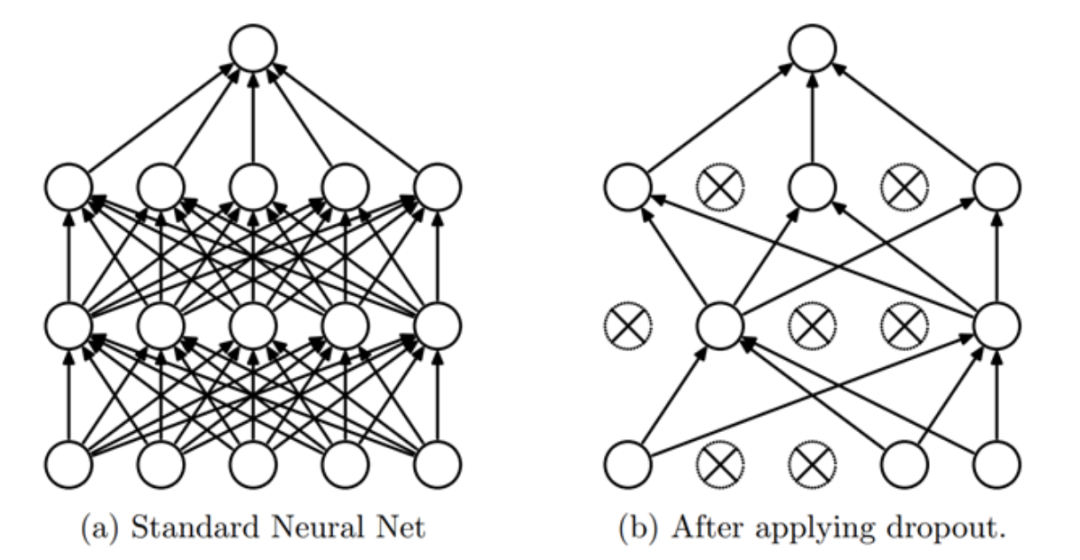
第二个优化技巧是Activation Regularization(AR, 激活正规化)，以及 Temporal Activation Regularization(TAR，临时激活正规化)，简单说这两个技巧的目的都是限制模型中各个权重的取值范围，使其趋向于较小的值。这可以有效地防止模型过度依赖少数特征或样本的噪声，从而提高模型的泛化能力和稳定性。在实践中，我们一般在Dropout之前应用TAR，而在Dropout之后应用AR。

第三个非常有用的技巧是Weight Tying, 我们的模型在输入层把Token映射为Embedding，而在输出层又把LSTM的输出映射回Token，所以一个直觉性的想法是可以让输入和输出层共享权重。

接下来让我们再次重构代码：

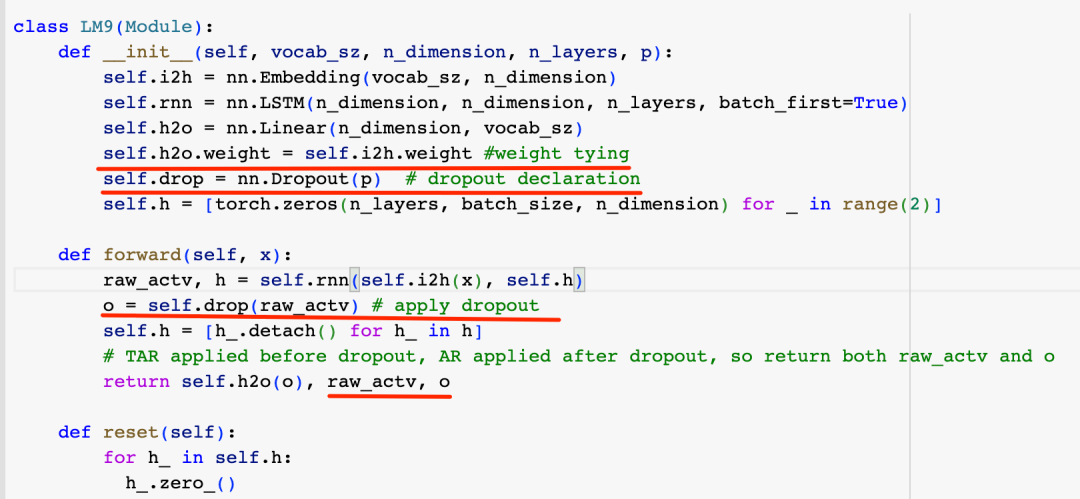
因为TAR是在Dropout之前应用，而AR是在Dropout之后应用，所以这里我们把应用Dropout之前和之后的激活权重都输出，除此之外，这里并没有直接应用TAR和AR优化技巧的代码，这是因为我们将使用fasi.ai提供的TextLearner类来训练模型，TextLearner会自动通过回调的方式帮我们应用这两个优化技巧，咱们再次训练模型看看效果：

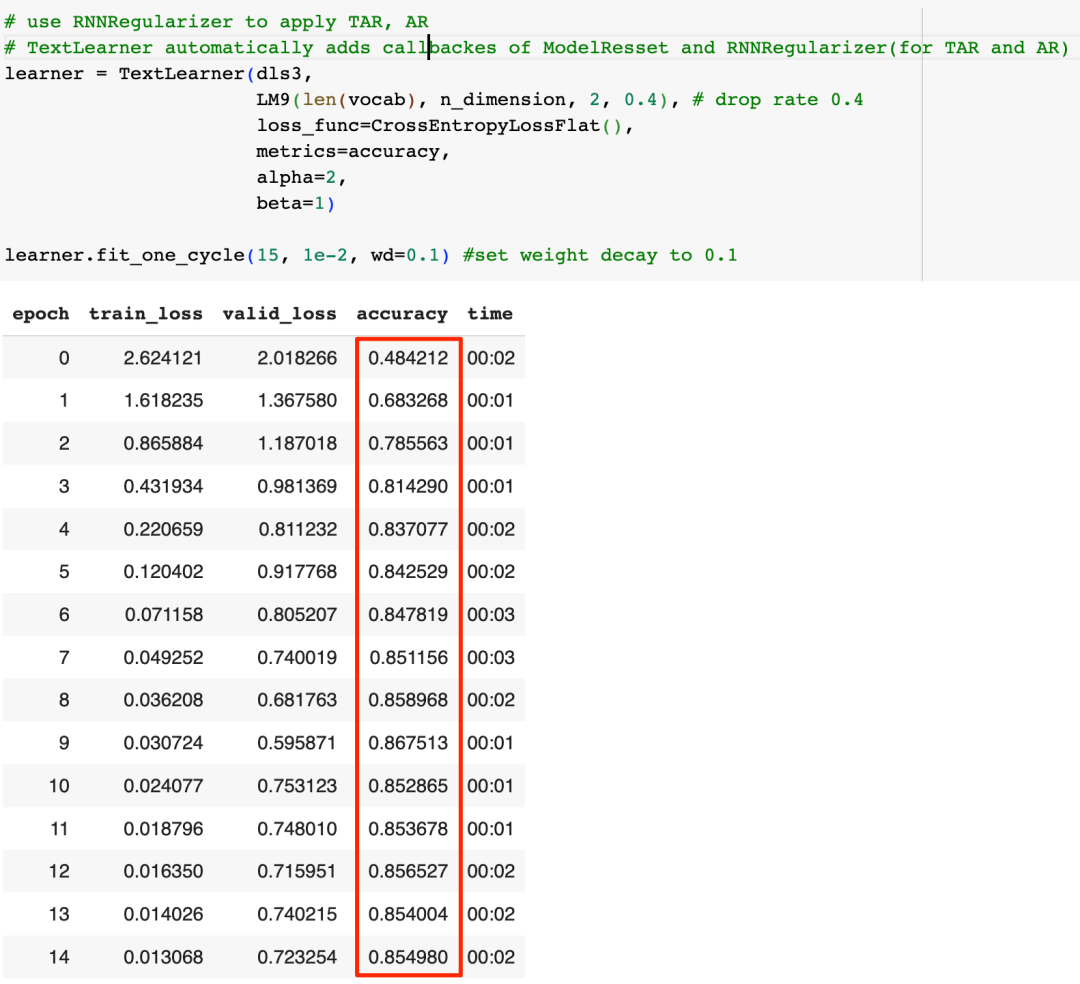
可以看到这些优化技巧的效果还是很明显的，模型的准确率被进一步提高到了85%左右，回忆一下，我们在上篇文章中提到过，瞎猜的准确率大约是15%，第一版的RNN准确率是49%，而借助LSTM，我们最终的准确率有了巨大的提升，达到了85%。

至此ChatGPT前传三部曲就结束了，总结一下，ChatGPT在业务中落地的成本不低，很多实际任务用更简单、更便宜的RNN架构就能解决得很好，基础版的RNN存在着短期记忆症的问题，而LSTM则通过给RNN引入长期记忆大幅提升了RNN的表现。任何复杂的事物背后都有一个简单的想法，虽然从N-Gram到RNN再到LSTM越来越复杂，但其背后体现的则是上下文越多，则预测越准确的这一朴素的思想。